Accuracy, Precision, Recall - Tradeoff is the name of the game.
Imagine we are creating a spam filter for an email system.
# ground fact
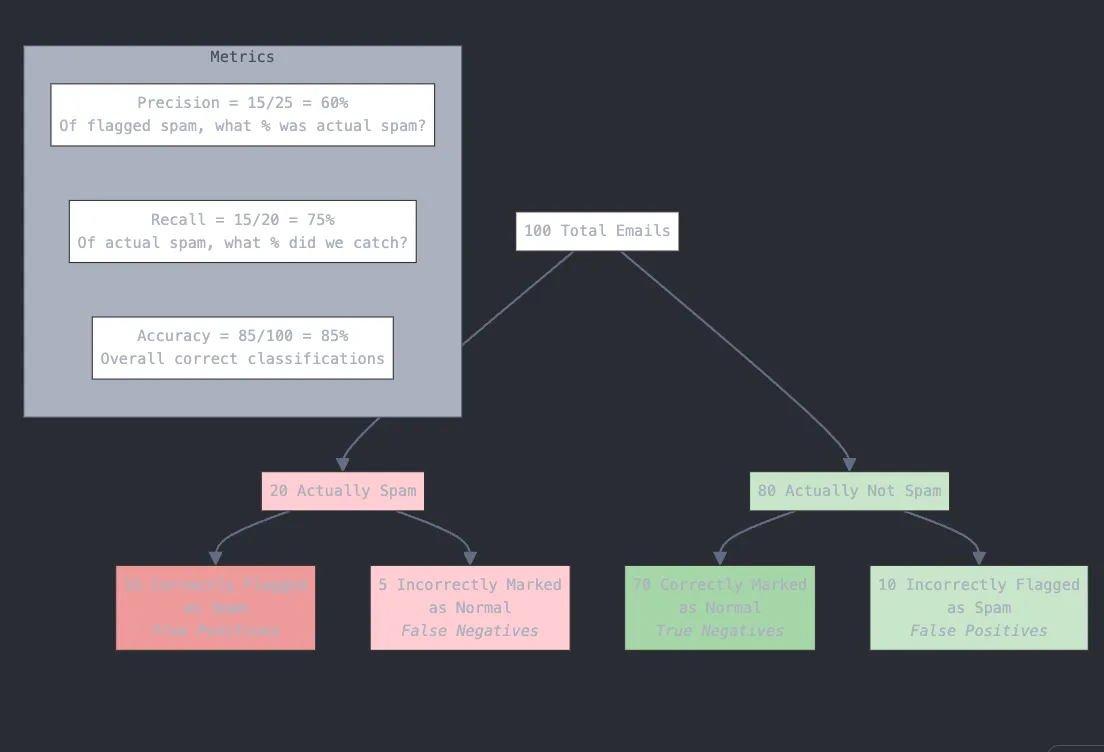
Out of 100 incoming emails, 20 are spam.
Our goal is to design the filter to correctly identify and flag these spam emails. Let’s say the filter produces these results:
# spam filter output
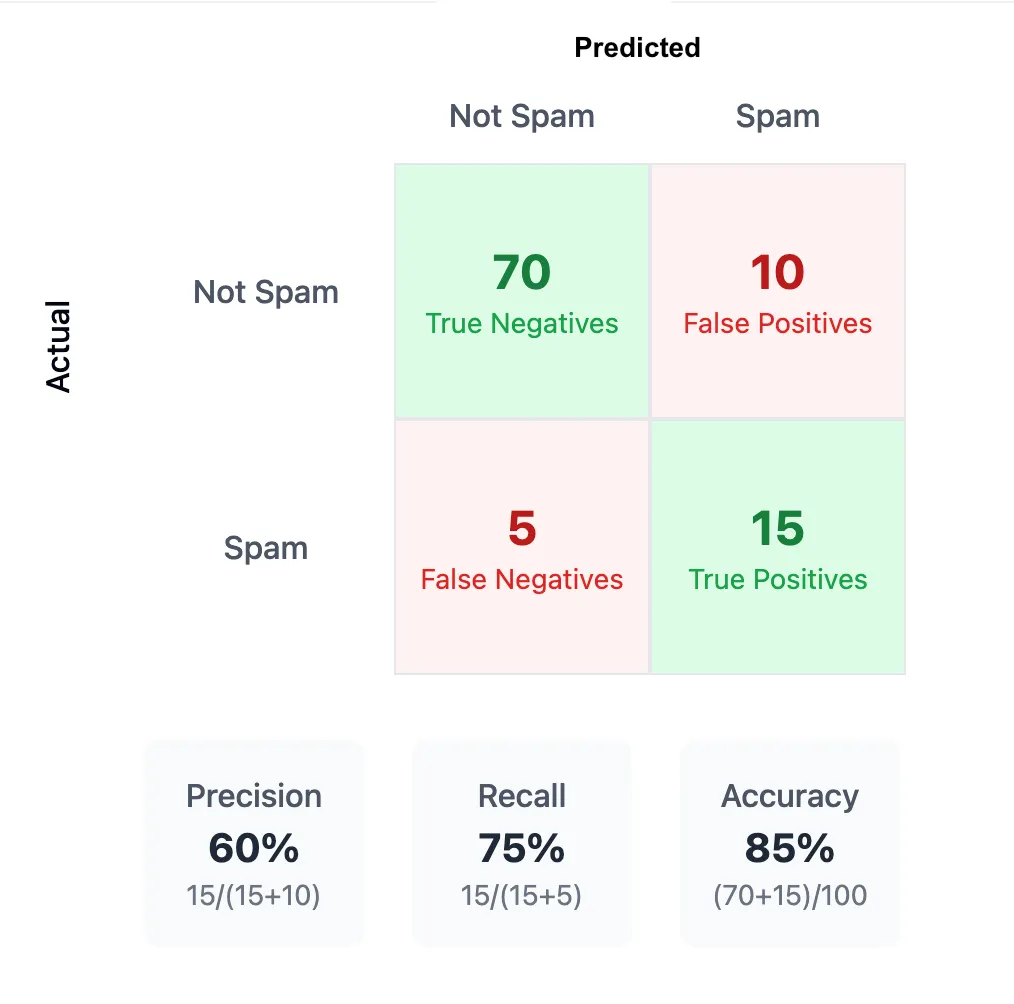
* Flagged 25 emails as spam
* Out of those 25 flagged emails, 15 were actually spam (true positives)
* This means 10 legitimate emails were incorrectly flagged (false positives)
* Did NOT Flag 5 emails as spam
* 5 actual spam emails were missed (false negatives)
Now we can break down the three concepts:
Precision
Precision answers: “Of all emails that were flagged as spam, what percentage was actually spam?”
Precision = 15 true positives ÷ 25 total flagged = 60%
Think of precision as how trustworthy the spam flags are. If we have high precision, when the filter says “this is spam,” it’s usually right.
Recall
Recall answers: “Of all actual spam emails, what percentage did it catch?”
Recall = 15 true positives ÷ 20 total actual spam = 75%
Think of recall as how thorough the filter is. High recall means we’re catching most of the spam, even if we sometimes flag legitimate emails too.
Accuracy
Accuracy answers: “Overall, what percentage of all emails did it classify correctly?”
Accuracy = (correctly identified spam + correctly identified non-spam) ÷ total emails = (15 + 70) ÷ 100 = 85%
Think of accuracy as overall correctness across all decisions.
The power of this example lies in the real-world tradeoffs it illustrates:
If we make the filter more aggressive, we’ll catch more spam (higher recall) but might annoy users by flagging legitimate emails (lower precision) If we make it more conservative, we’ll have fewer false alarms (higher precision) but might miss some spam (lower recall)
These tradeoffs help explain why even modern spam filters aren’t perfect - they’re constantly balancing these competing metrics.